Alphanumerisch

Funktionsweise und Beispiel

Each letter has a specific position in the alphabet. A is the first letter and gets the value 1, B is the second one with the value 2, this runs up to Z which is has the value 26. Of course other methods counting are also possible.
So you can simply move values. With an offset of 2 A has the value (normal value 1 + offset 2) = 3 and Z = 26 + 2 = 28 It is also possible to rotate the values, ie A = 26 and Z = 1 The most common and easiest option (A = 1, Z = 26) is very common in Multis and Mysteries as a simple number encryption.

With these numbers a lot of calculations are possible, such as the addition of the letter values. Therefor easy calculation like checksum are shown as an additional feature. A cross-sum (or sum of digits) is defined as the sum of the digits of a number Thus for a value n = 36 036 the decimal digit sum q (n) = 3 + 6 + 0 + 3 + 6 = 18

In geocaching cross sums are often used to calculate a value from a string of letters. This is very popular with Multis. For each letter the associated numerical value is taken and then added up.

Accordingly, the cross product is formed by multiplying the digits.

Note: Since there are different kinds of checksum calculation, one must read carefully what is actually wanted in the cache description!

Examples:

Examples of case values:

Mode letter to number, forward, offset 0: ABC = 1 2 3
Mode letter to number, forward, offset -10: ABC = (1 - 10) (2 - 10) (3 - 10) = -9 -8 -7
Mode letter to number, reverse, offset 10: ABC = (26 + 10) (25 + 10) (24 + 10) = 36 35 34
Mode letter to number, reverse, offset -100: ABC = (26 - 100) (25 - 100) (24 - 100) = -74 -75 -76
Mode number to letter, forward, offset 0: 1 2 3 = ABC
Mode number to letter, reverse, offset -100: -74 -75 -75 = (-74 + 100) (-75 + 100) (-75 + 100) = 26 25 24 = ABC

Example for cross sums (for the simple mode A = 1, Z = 26):
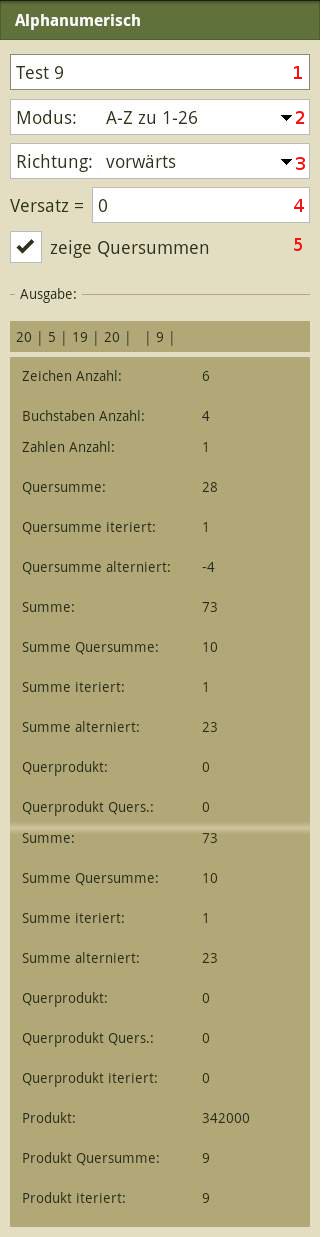
If A = 1 ,.. Z = 26, then for the text "TEST 9", these numbers 20, 5, 19, 20, [BLANK] 9 will be derived. This results in:

Char Count: 6
Letter Count: 4
Digit Count: 1
Cross Total: 2 + 0 + 5 + 1 + 9 + 2 + 0 + 9 = 28
Cross Total Iterated, each result of a cross-sum will be calculated again as cross-sum until the result only has one digit left: 28 -> 2 + 8 = 10 -> 1 + 0 = 1 (also called 'one-digit cross sum')
Cross Total Alternating, is to alternate addition and subtraction the digits of a number starting with the last character: 9 - 0 + 2 - 9 + 1 - 5 + 0 - 2 = -4
Sum: 20 + 5 + 19 + 20 + 9 = 73
Sum Cross Total: 73 -> 7 + 3 = 10
Sum Iterated: 73 -> 7 + 3 = 10 -> 1 + 0 = 1
Sum Alternating: 9 - 20 + 19 - 5 + 20 = 23
Cross Product: 2 * 0 * 6 * 1 * 9 * 2 * 0 * 9 = 0
Cross Product Cross Total: 0 (assuming the cross-sum was 83, this would result in: 8 + 3 = 11)
Cross Product Iterated: 0 (assuming the cross-sum was 83, this would result in: 8 + 3 = 11 -> 1 + 1 = 2)
Product: 20 * 5 * 19 * 20 * 9 = 342000
Product Cross Total: 3 + 4 + 2 + 0 + 0 + 0 = 9
Product Iterated: 9 (assuming the cross-sum of the product was 10, this would result in: 10 = 1 + 0 = 1)

Source: Wikipedia

Operation

It is possible to convert text to numbers (letters to their number value, numbers remain numbers, special characters are ignored, except for "number of character"). The feature reverse direction numbers to text works the same way.
There you will get for any number the assigned letter. Here the cross-sum works as well because the number entries will be calculated.

Input

Letters or numbers to be calculated. In mode (1-26 to A-Z) spaces must be made between the letter values, as for 123 it can not be distinguished whether or ABC (12 = L) C or A (23 = W).
Mode (A-Z to 1-26, ie text to numbers, or 1-26 to A-Z, ie numbers to text). Note: The choice of mode should be done first, because it clears the field of digits!
Direction of the calculation (forward: A = 1 and Z = 26, reverse: A = 26 and Z = 1)
Enter offset that will be added to determined result
Checkbox whether checksums should be displayed.

Output
Calculated numbers - or letters and if necessary checksums of the determined sequence of numbers (for explanation see functional description of "checksum")