Römische Zahlen

Funktionsweise und Beispiel

Römische Zahlen sind die Zahlzeichen einer in der römischen Antike entstandenen und noch heute für Nummern und besondere Zwecke gebräuchlichen Zahlschrift, in der in der heutigen Normalform die lateinischen Buchstaben I (1), V (5), X (10), L (50), C (100), D (500) und M (1000) als Zahlzeichen für die Schreibung der natürlichen Zahlen verwendet werden. Es handelt sich um eine additive Zahlschrift, aber ohne Stellenwertsystem und ohne Zeichen für Null. Zugrunde liegt ein kombiniert quinär-dezimales oder biquinäres Zahlensystem mit den Basiszahlen 5 und 10.

Bei der einfachen Umrechnung werden die Zahlwerte einfach addiert. Dabei werden Zahlen mit so wenig Zeichen wie möglich dargestellt, beginnend mit dem höhsten Wert links. Eine Zehn wird also nicht mit zehn Einsen dargestellt sondern mit einer Zehn (entspricht X). Generell kann man sagen: Wenn noch ein hohes Zeichen "rein passt", nimm es: In 1200 passt ein M = 1000 noch rein, in die restlichen 200 passt ein D = 500 nicht mehr aber noch C = 100 und noch eines.
Erst im Mittelalter wurde diese Form durch die heute am meisten bekannte und am häufigsten genutzte Subtraktionsregel ergänzt. Danach dürfen direkt vor einem X und einem V ein einzelnes I stehen; ebenso wie vor einem L und C ein einzelnes X und vor einem D und einem M ein einzelnes C stehen darf. Es werden also die neuen "Zahlen" IV (4), IX (9), XL (40), XC (90), CD (400) und CM (900) eingeführt. Wenn also ein niedrigeres Zeichen vor einem höheren kommt, wird dieses vom höheren subtrahiert. IV ist also (V - I) = (5 - 1) = 4. Diese neue Regel soll verhindern, dass vier gleiche Zeichen hintereinander kommen. So ersetzt IV jetzt IIII.

Später fanden sich zwei Abweichungen dieser Form. Erstens fand man die Möglichkeit, ein doppeltes niedriges Zeichen voranzusetzen und zu subtrahieren. Also IIV = (5 - 1 - 1) = 3. Außerdem gab es Fälle bei denen die Subtraktion von I und X auch von allen höheren Werten erfolgen konnte, wie IL = (50 - 1) = 49 oder IM = (1000 - 1) = 999. Um die Verwirrung perfekt zu machen, konnten beide Ausnahmefälle auch kombiniert auftreten.

Beispiele

Einfache Umrechnung:
1984 = 1 * 1000 + 1 * 500 + 4 * 100 + 1 * 50 + 3 * 10 + 4 * 1 = 1 * M + 1 * D + 4 * C + 1 * L + 3 * X + 4 * I = MDCCCCLXXXIIII

Mit Subtraktionsregel (Gängigste Variante!):
Ersetze:

IIII --> IV
VIIII --> IX
XXXX --> XL
LXXXX --> XC
CCCC --> CD
DCCCC --> CM

--> 1984 = MDCCCCLXXXIIII (einfache Umrechnung) = M(DCCCC)LXXX(IIII) = M(CM)LXXX(IV) = MCMLXXXIV

Mit "doppelter" Subtraktionsregel:
Ersetze zusätzlich:

III --> IIV
VIII --> IIX
XXX --> XXL
LXXX --> XXC
CCC --> CCD
DCCC --> CCM

--> 1984 = MCMLXXXIV (einfache Subtraktionsregel) = MCM(LXXX)IV = MCMXXCIV

Mit "erweiterter" Subtraktionsregel:
XM = (1000 - 10) = 990; anstelle von CMXC = (CM)(XC) = (1000 - 100) + (100 - 10) = 990

Beide Sonderformen vereint:
--> 1984 = 1000 + 980 + 4 = M(XXM)(IV) = MXXMIV
--> Es wird also X statt des regulär erlaubten C von M abgezogen, und das sogar doppelt.

Chronogramm-Sonderform:
Aufgrund der Chronogramm-Funktion (s.u.) gibt es bei GCC noch die Form, dass einfach alle gefundenden römischen Zahlzeichen aufaddiert werden, unabhängig ihrer Lage, und ohne irgendwelche Subtraktionen. Wenn also in dem Text insgesamt 4mal I, 3mal X, 1mal L, 4mal C, 1mal D und einmal M vorkommen, wird 1984 ausgegeben:

1984 = MDCCCCLXXXIIII = IMXXCLIXDICCIC = ...
MXXMIV = 1000 + 10 + 10 + 1000 + 1 + 5 = 2026

Quelle: Wikipedia

Ein Chronogramm ist ein Satzteil, ein Satz, ein Sinnspruch oder eine Inschrift, meist in lateinischer Sprache, bei der alle darin vorkommenden Buchstaben, die zugleich römische Zahlensymbole sind (I, V, X, L, C, D, M), addiert die Jahreszahl des Ereignisses ergeben, auf das sich der Text des Chronogramms bezieht. Es werden alle Zahlenwertbuchstaben entgegen der sonst üblichen Zählmethode einzeln erfasst, eine Subtraktion des kleineren vom größeren Zahlenwert erfolgt nicht. Die Zahlensymbole werden meist hervorgehoben, etwa durch Erhöhung oder Verdickung der Buchstaben bzw. durch farbliche Abhebung mittels Rötung oder Vergoldung.

Im "natürlichen Chronogramm" stehen die Zahlzeichen darüber hinaus in der richtigen Reihenfolge, z. B. AMORE MATVRITAS = MMVI = 2006.

Quelle: Wikipedia

Bedienung

Groß- und Kleinschreibung macht keinen Unterschied!

Eingabe

Übersetzen römischer Zahlen
Chronogramm
Tabelle der römischen Zahlen

Ausgabe

Übersetzen römischer Zahlen

Bei dieser Funktion werden römische Zahlen umgerechnet. Bei der Berechnung von normalen Zahlen ins römische System ("Nummern zu Römisch") wird die normale Subtraktionsregel verwendet. Bei ("Römisch zu Nummern") gibt es folgenden Ablauf:

Kann die Eingabe in normaler Subtraktionsform interpretiert werden?
Sonst: Kann sie als Form der einfachen Umrechnung angesehen werden?
Sonst: Kann sie als eine der Sonderformen interpretiert werden? Ggf. Ausgabe als Ergebnis einer der Subtraktions-Sonderformen ("doppelt", "erweitert", Kombination) und Ausgabe als einfache Aufaddierung.

Eingabe

zu übersetzende Zahl
Auswahl, ob eine römische oder eine lateinische Zahl übersetzt werden soll

Ausgabe

die ermittelte Zahl (lateinisch oder römisch)
Bei römischer Eingabe: Liegt die Eingabe in der einfachen Form oder mit der einfachen Subtraktionsregel vor, wird das umgerechnete Ergebnis ausgeben.
Liegt sie in einer anderen Form vor, wird die Eingabe als "ungültig" angesehen. Zusätzlich werden mögliche Zahlen ausgegeben, Berechnungen mit den oben beschriebenen Sonderformen:
Beispiel: Eingabe "MXXMIV" führt zu Ausgabe "1984" (wg. Kombination beider Subtraktionssonderformen, s.o.) und "2026" (Aufaddierung, s.o.)

Chronogramm

Aus normalem Text, werden römische Zahlzeichen extrahiert und aufaddiert.

Eingabe

Eingabe des Textes

Ausgabe
Ergebnis der Aufaddierung der Wertigkeiten aller M, D, C, L, X, V, I

Tabelle der römischen Zahlen

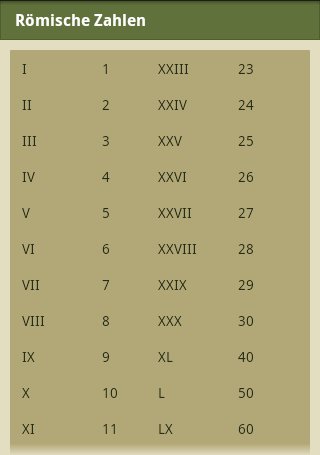
Eingabe
-
Ausgabe
Tabelle