vorherigerMenunächster

Primzahlen

Funktionsweise und Beispiel

Eine Primzahl ist eine natürliche Zahl, die größer als Eins und nur durch sich selbst und durch Eins teilbar ist. Eine Primzahl ist also eine natürliche Zahl mit genau zwei natürlichen Zahlen als Teiler. Die kleinsten Primzahlen sind 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97

Bei der Primfaktorzerlegung wird eine natürliche Zahl als Produkt aus Primzahlen dargestellt. Die Primfaktorzerlegung der Zahl 45 ergibt 3 * 3 * 5.

Quelle: Wikipedia

Bedienung



Alle nachfolgenden Funktionen verzweigen auf eine einheitliche Eingabeseite - diese wird daher nur einmal dokumentiert. GCC arbeitet mit Primzahlen bis 1.000.000

Eingabe
  1. Primzahl an n.ter Position ermitteln; Beispiel: Die 5. Primzahl ist 11
  2. Die zu einer Zahl nächstgelegene Primzahl ermitteln; Beispiele: Die der 22 nächstgelegene Primzahl ist 23. Die der 42 nächstliegenden Primzahlen sind 41 und 43.
  3. Position einer Primzahl ermitteln; Beispiel: Die 5 ist die 3. Primzahl
  4. Prüfen, ob eine Zahl eine Primzahl ist; Beispiele: Die 23. ist eine Primzahl, die 42 ist keine Primzahl.
  5. Zerlegen einer Zahl in Primfaktoren; Beispiel: 42 = 2 * 3 * 7
Ausgabe

Ermitteln des gewünschten Wertes



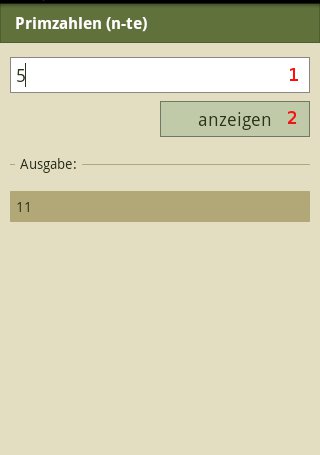
Eingabe
  1. Eingabe des entsprechenden Zahlenwertes
  2. Ausführen der Berechnung
Ausgabe
Anzeige des ermittelten Zahlenwertes oder einer Fehlermeldung, wenn die eingegebene Zahl keine Primzahl ist