vorherigerMenunächster

Koordinaten

Funktionsweise und Beispiel

Unter dem Begriff “Koordinate” versteht man die Angabe der Lage eines Punktes relativ zu einem Bezugspunkt. Ein Punkt auf einem Lineal kann die Koordinate “3cm” haben, was so viel heißt, wie dass der Punkt 3cm von seinem Bezugspunkt, dem Beginn des Lineals bei 0, entfernt ist. Bei zwei Dimensionen, wie einer Karte, braucht man auch zwei Angaben, um den Punkt richtig bestimmen zu können: Wie weit links/rechts und oben/unten der Punkt sich von dem Nullpunkt entfernt befindet. Dieses System kann man unendlich ausweiten, in der Praxis sind jedoch selten mehr als dreidimensionale (also Koordinaten im Raum, mit drei Angaben) Punkte von Relevanz.

Geografische Koordinaten sind Punkte, in einem geografischen (erdbezogenen) Kontext. Sie beschreiben Punkte bezüglich ihrer Lage auf der Erde. Da es sich dabei um die Angabe von Orten auf der Erdoberfläche handelt, benötigt man dazu genau zwei Werte, sie sind also zweidimensional. Veranschaulichen kann man sich diesen Umstand auf einer (flächigen) Karte. Dort reichen jeweils zwei Werte aus, um eine Stadt oder ähnlieches zu finden.

Geografische Koordinaten werden allerdings nicht in Metern oder anderen Längeneinheiten angegeben, da die Erde keine Ebene ist. Man spricht vielmehr von sphärischen Körpern, hier zum anfänglichen Verständnis erstmal eine Kugel. Daher ist sie in ein Gitternetz eingeteilt. Die Erde wird dabei in 360 Längengrade und 180 Breitengrade aufgeteilt, also in mathematische Winkel. Längengrade verlaufen “senkrecht” durch Nord- und Südpol, Breitengrade “waagerecht”. Dabei stellt der Äquator den längsten Breitengrad dar, da dieser die dickste Stelle der Erde markiert. Daher ist der Äquator auch der nullte Breitengrad. Von ihm aus werden anderen Breitengrade nach Norden und Süden gezählt. Die Pole, also die nördlichste bzw. südlichste Stelle der Erde, liegen bei 90° Nord bzw. Süd. Die Längengrade werden von einem willkürlichen Nullmeridian nach Osten und Westen gezählt bis jeweils 180°. Es wurde festgelegt, dass der Nullmeridian durch Greenwich/London, UK, läuft.

Einen Ort kann man also auf der Erde anhand von zwei Gradzahlen bestimmen: Wie viel Grad er von Greenwich nach Osten oder Westen liegt und wie viel Grad nach Norden oder Süden er von Äquator entfernt liegt.

Nun muss man allerdings bedenken, dass die Erde keine Kugel ist, und daher mathematische Berechnungen auf der Oberfläche (wie zB.: Wie lang ist der Weg von A nach B auf der Oberfläche, auch einfach bekannt als Distanz zwischen zwei Orten) nicht identisch sind, mit den verhältnismäßig einfachen Kugelberechnungen. Vielmehr nutzt man dafür ein anderes geometrisches Objekt, den so genannten Ellipsoiden. Das ist im Grunde eine abgeflachte Kugel. Leider sind auf solch einem Objekt die Berechnungen unverhältnismäßig komplexer. Würde man einfach eine Kugel nehmen, könnten Fehler um bis zu 20km Unterschied bei Ortsbestimmungen entstehen.

Da aber auch ein Ellipsoid nur eine Näherung ist, da die Erde, bedingt durch Gebirge und Meerestiefen, nicht komplett eben ist, kommt es auch hier an verschiedenen Orten zu unterschiedlichen Rechenabweichungen. Deshalb kommen im hochpräzisen geodätischen Bereich lokal angepasste, besondere Ellipsoiden zum Einsatz. Im mitteleuropäischen Raum kann man den Bessel-Ellipsoiden nennen.

International wird heute jedoch meist der WGS84-Ellipsoid (World Geodetic System 1984) benutzt, der die aktuell beste durchschnittliche Näherung für die gesamte Erde darstellt. Dieses System kommt auch beim GPS (Global Positioning System) und Geocaching zur Anwendung.

Die GPS-Koordinaten eines Punktes werden in Grad (°), Minuten (') und Sekunden (") angegeben. Dabei gilt wie bei der Uhrzeit: 1° = 60' und 1' = 60". Mögliche Darstellungen sind:Und noch ein Merksatz: "N" (bzw. "S") ist der Breitengrad (Latitude), "O" (bzw "W) ist der Längengrad (Longitude).

Quelle: Wikipedia

Geocaching und Koordinatenprojektion

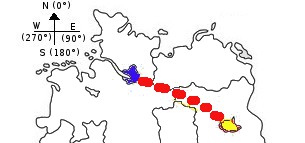
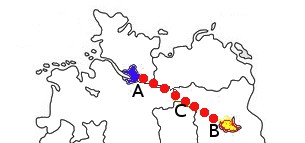
In vielen Mysteries ist es erforderlich, eine Projektion durchzuführen. Um hierfür ein Verständnis zu schaffen, soll das grundsätzliche Vorgehen an einem Beispiel erläutert werden. Die Projektion setzt sich zusammen aus einer Winkel- und einer Entfernungsangabe. Um die Winkelangabe zu verstehen, kann man sich den Kompass mit folgenden Winkelangaben vorstellen Steht man nun in Hamburg (blaue Markierung) und will nach Berlin (rote Markierung) projizieren (gelbe Linie), so ist die Winkelangabe ca. 115° und die Entfernung 256 km.

Von Berlin aus findet man den Standort in Hamburg, indem man die Projektion mit einer Winkelangabe von ca. 298° macht und - Überraschung!! - ebenfalls 256 km.

Bedienung

Anmerkung zur Bedienung

In den nachfolgenden Beschreibungen kann für jede Koordinate zuerst das Koordinaten-Formates ausgewählt werden: Danach folgt die Eingabe des Breiten- und Längengerades für die jeweilige Koordinate. Bei DEC wird nur ein Vorzeichen anstelle von N/S bzw. O/W verlangt. Es gilt: Süd und West sind negative Werte, Nord und Ost entsprechend positiv.

Eingabe
  1. Winkel zweier Koordinaten zueinander berechnen
  2. Konvertieren zwischen verschiedenen Koordinatenformaten
  3. Entfernung zwischen zwei Koordinaten berechnen
  4. Geohash (Längen-/Breitengrad-Georeferenzierung)
  5. Berechnen des Schnittpunktes anhand von Winkel
  6. Berechnen des Schnittpunktes anhand von Entfernungen (Zwei)
  7. Berechnen des Schnittpunktes anhand von Entfernungen (Drei)
  8. Berechnen des Schnittpunktes anhand von Winkel und Entfernung
  9. Berechnen des Schnittpunktes anhand von zwei Linien aus vier Punkten
  10. Ermitteln des Mittelpunktes zweier Koordinaten
  11. Projektion einer Koordinate auf eine angegebene Entfernung

Winkel zweier Koordinaten zueinander berechnen

Hat man zwei Punkte A und B mit ihren Längen- und Breitengraden gegeben, kann man berechnen, in welche Richtung B von A aus liegt und andersrum. Ein Beispiel dafür wäre, wenn man wissen will in welcher Richtung Hamburg liegt, wenn man in Berlin steht. Als Referenz dient auch hier der Kompass. Wird also 0° ausgegeben, würde sich Hamburg also direkt im Norden befinden – was es bekanntlich nicht tut :)

Auf einer einfachen Ebene wären die Hinrichtung und die Rückrichtung genau um 180° (eine halbe Umdrehung) verschieden. Dieses Ergebnis wird es bei sphärischen Berechnungen nicht geben. Dort kommt es zu Abweichungen aufgrund der Krümmung.


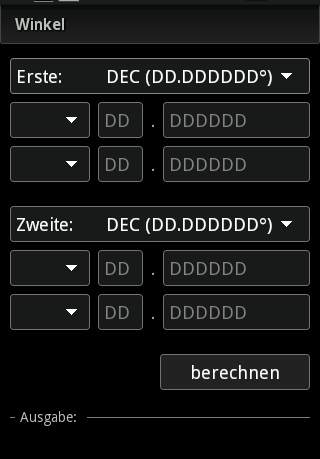
Eingabe
  1. Eingabe Informationen zur ersten Koordinate
  2. Eingabe Informationen zur zweiten Koordinate
  3. Berechnung starten
Ausgabe
Die errechneten Winkel der Hin- und Rückrichtung bezogen auf Nord = 0°.

Konvertieren zwischen verschiedenen Koordinatenformaten

Umrechnung von DEC in DEG oder Umwandlung anderer Formate. DEC, DEG und DMS sind stark miteinander verwandt. Beispiele: Analog ist die Rückrichtung: Die Umrechnung in UTM und MGRS sind ungleich komplexer und können in entsprechender Fachliteratur nachgelesen werden.

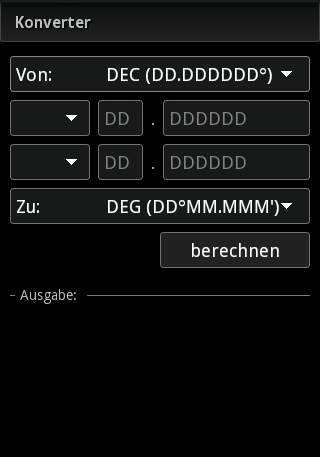
Eingabe
  1. Eingabe Informationen zur ersten Koordinate
  2. Auswahl des gewünschten Koordinatenformates
  3. Berechnung starten
Ausgabe
Ins gewünschte Format konvertierte Koordinate

Entfernung zwischen zwei Koordinaten berechnen

Diese Funktion gibt einfach die kürzeste Distanz zwischen zwei Punkten aus. Dabei ist es egal, welcher der Ausgangs- und welcher der Zielpunkt ist.

Eingabe
  1. Eingabe Informationen zur ersten Koordinate
  2. Eingabe Informationen zur zweiten Koordinate
  3. Berechnung starten
Ausgabe
Distanz zwischen den Koordinaten

Geohash (Längen-/Breitengrad-Georeferenzierung)

Sinn des Geohash ist es, die Koordinaten eines Punktes mit einem kurzen und eindeutigen Identifier anzugeben, sodass die Koordinatenangabe in eMails, Foren etc. einfacher ist. Entwickelt wurde er von Gustavo Niemeyer, es wurde auf geohash.org publiziert. Die Berechnung erfolgt über eine Umwandlung der Koordinaten in Base32 und einer weiteren Umwandlung von dessen Binärwerten.

Eingabe
  1. Auswahl des Modus (kodieren, dekodieren)
  2. Eingabe der Koordinate (mit Formatauswahl) oder des Geohash
  3. Auswahl des Koordinatenformates (bei dekodieren)
  4. Berechnung starten
Ausgabe
Geohash oder Koordinate im gewünschten Format

Berechnen des Schnittpunktes anhand von Winkel



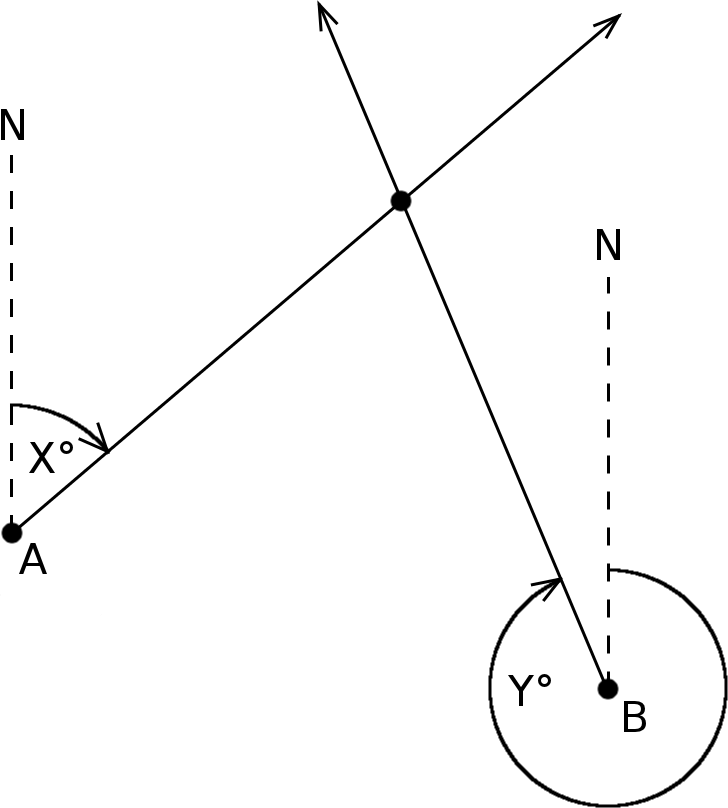
Dieser Berechnung liegt die klassische “Kreuzpeilung” zugrunde, wie sie vor allem in der Seefahrt genutzt wird. Ein Schiff kann seine Position bestimmen, indem es zwei feste Punkte anpeilt – also mit dem Kompass ausmisst, in welcher Richtung sie liegen. So kann also der Leuchtturm bei 270° liegen und die Boje bei 15°. Das ergibt einen eindeutigen Punkt. Würde das Schiff jetzt weiter fahren, würde sich auch die Richtung des Turms und der Boje ändern. Diese Funktion macht die Umkehrung: Sie sucht das Schiff. Man weiß also, das Schiff liegt in soundso viel Grad vom Leuchtturm aus und in soundsoviel Grad von der Boje. Gedanklich könnte man eine (ausreichend lange) Schnur von Leuchtturm und Boje in die entsprechende Richtung legen. Dort, wo sich die beiden Schnüre treffen, befindet sich also das Schiff – oder natürlich noch sehr viel besser: Der Cache! :)


Eingabe
  1. Eingabe Informationen zur ersten Koordinate
  2. Angabe des Winkels (in Grad)
  3. Eingabe Informationen zur zweiten Koordinate
  4. Angabe des Winkels (in Grad)
  5. Auswahl des Formates der ermittelten Koordinate
  6. Berechnung starten
Ausgabe
Koordinate des errechneten Schnittpunktes

Berechnen des Schnittpunktes anhand von Entfernungen



Zwei Punkte

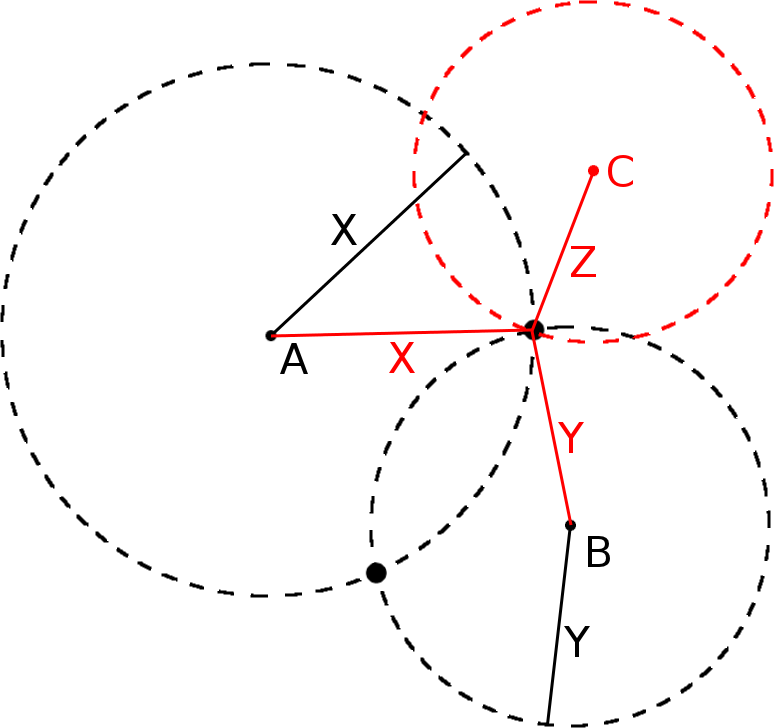
Um diese Funktion zu verstehen, tun wir einfach einmal so, als würden wir uns wirklich auf einer Ebene bewegen, beispielsweise einer Karte. Wir wissen nun, dass der Cache irgendwo liegt. Wir haben allerdings nur zwei Informationen: Er ist X Meter von der Birke und Y Meter von der Eiche entfernt. Nun gibt es aber ein Problem: Angenommen, wir würden an der Birke stehen. Wir wüssten zwar, dass wir X Meter weit gehen müssen, doch in welche Richtung? Genauso verhält es sich mit der Eiche. Wir suchen also den Punkt, der beide Bedingungen erfüllt. Wir machen wird das? Nun, einfach gesagt, können wir auf unserer Karte die Birke suchen, und um sie einen Kreis malen, mit dem Radius X. Alle Punkte des Kreises sind die möglichen Punkte, die genau X Meter von der Birke weg sind. Das gleiche erhält man, wenn man das gleiche mit der Eiche macht. Und wenn wir nun Glück haben, berühren sich die beiden Kreise in einem Punkt. Dieser Punkt ist also Teil des Birken- als auch des Eichenkreises, ist also X Meter von der Birke, als auch Y Meter von der Eiche weg.

Wahrscheinlicher ist jedoch, dass sich beide Kreise entweder gar nicht schneiden (das wäre doof, da solltet ihr besser noch einmal in die Aufgabenstellung schauen *gg*) oder gleich in zwei Punkten. Welcher Punkt ist es denn nun? Das kann man leider nicht sagen. Da heißt es: Ausprobieren. Es sei denn...

Drei Punkte

ihr habt noch eine Angabe, einen dritten Punkt. Muss der Cache nicht vielleicht auch noch Z Meter von der Kiefer weg sein? Denkt euch jetzt also noch einen dritten Kreis um die Kiefer. Wenn ihr Glück habt, verläuft dieser durch einen der ersten beiden Schnittpunkte.

Anmerkungen:
  1. Aufgrund von Mess- aber auch Rechenungenauigkeiten kann die Berechnung mit dem dritten Kreis nur genähert werden: Durch falsche Einmessungen oder ungenaue Koordinatenangaben, verläuft der Kreis vielleicht nicht exakt durch einen Schnittpunkt, sondern 1 Meter vorbei. Hier ist es dem Nutzer vorbehalten, zu sagen, wann ein Schnittpunkt noch akzeptabel ist, das ist die Toleranz.
  2. Auch die Drei-Punkte-Methode kann in einem Sonderfall zu zwei Schnittpunkten führen, nämlich genau dann, wenn der dritte Punkt genau auf der gedachten Verbindungslinie der ersten beiden Punkte liegt. Dann gibt es entweder keinen oder zwei Schnittpunkte der drei Kreise.


Eingabe
  1. Eingabe Informationen zur ersten Koordinate
  2. Angabe des Entfernung sowie der Einheit der Entfernung [m, km, nm, ft]
  3. Eingabe Informationen zur zweiten Koordinate
  4. Angabe des Entfernung sowie der Einheit der Entfernung [m, km, nm, ft]
  5. Auswahl des Formates der ermittelten Koordinate
  6. Berechnung starten
Ausgabe
Zwei Punkte
Sofern vorhanden, Koordinate des berechneten Schnittpunktes bzw. die Koordinaten der zwei Schnittpunkte.
Drei Punkte
Normale Ausgabe: Wird ein Schnittpunkt/werden mehrere Schnittpunkte innerhalb der angegebenen Toleranz gefunden, werden deren Koordinaten ausgegeben.
Erweiterte Ausgabe: In der Berechnung werden je zwei Kreise miteinander geschnitten. Dadurch bekommt man im Extremfall 6 Schnittpunkte. Zu allen ermittelten Schnittpunkten wird die Distanz zur jeweils dritten Koordinate ermittelt.Die erweiterte Ausgabe gibt alle ermittelten Schnittpunkt-Koordinaten aus, inklusive ihrem Abstand zur dritten Koordinate, angegeben als "Toleranz". Liegt dieser Abstand innerhalb der angegebenen Toleranz, wird dieser Schnittpunkt als "Treffer" angesehen. Die Schnittpunkte sind aufsteigend nach ihrer Toleranz sortiert.

Berechnen des Schnittpunktes anhand von Winkel und Entfernung



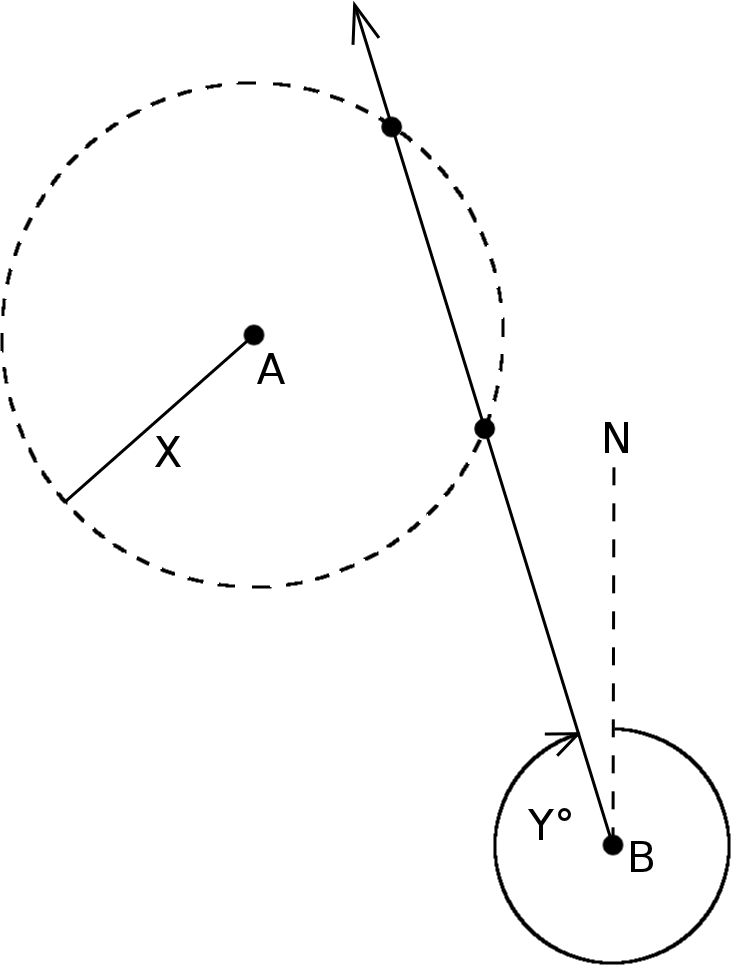
Das Szenario hier sieht wie folgt aus: Man weiß, dass der Cache in X Metern Entfernung zu einem bestimmten Ort A, beispielsweise einem Haus, liegt. Allerdings weiß man nicht, in welche Richtung. Man könnte nun einen Kreis um das Haus ziehen, mit dem Radius von X. Irgendwo auf dem Kreis muss nun der Cache liegen. Nun hat man aber noch eine zweite Information: Vom Schornstein (oder einem anderen Punkt B), muss man in Y Grad laufen. Allerdings gibt es nun keine Angabe, wie weit. Nun läuft man also in Richtung Y. Wenn man Glück hat, überquert man dann plötzlich den vorher gezeichneten Kreis. Das ist dann die Stelle, wo der Cache liegt: Genau X Meter vom Haus weg und vom Schornstein aus in Y Grad.

In den meisten Fällen werden zwei Schnittpunkte berechnet werden, da der Richtungsstrahl meist durch den Entfernungskreis durchläuft (man spricht von einer Sekante). In seltenen Fällen streift dieser tatsächlich nur in einem Punkt, dann ist es eine Tangente. Bei fehlerhafter Aufgabenstellung (falsches Lesen kommt ja gar nicht in Frage!) gibt es keinen Schnittpunkt. Dann ist der Richtungsstrahl eine Passante.

Eingabe
  1. Eingabe Informationen zur ersten Koordinate
  2. Angabe des Winkels (in Grad)
  3. Eingabe Informationen zur zweiten Koordinate
  4. Angabe des Entfernung sowie der Einheit der Entfernung [m, km, nm, ft]
  5. Auswahl des Formates der ermittelten Koordinate
  6. Berechnung starten
Ausgabe
Koordinate(n) des/der ggf. errechneten Schnittpunkte(s)

Ermitteln des Mittelpunktes zweier Koordinaten

In der nachfolgenden Grafik werden die Koordinaten des Punktes C ermittelt, der in der Mitte zwischen den Punkten A und B liegt.



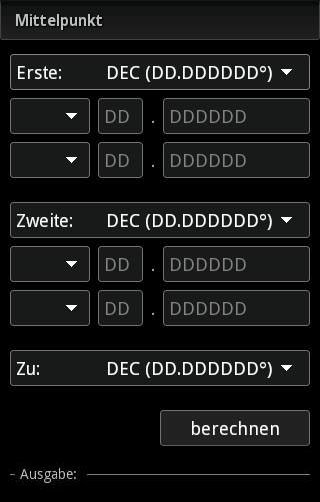
Eingabe
  1. Eingabe Informationen zur ersten Koordinate
  2. Eingabe Informationen zur zweiten Koordinate
  3. Auswahl des Formates der ermittelten Koordinate
  4. Berechnung starten
Ausgabe
Koordinate des errechneten Mittelpunktes

Projektion einer Koordinate auf eine angegebene Entfernung

Siehe Beispiel im Abschnitt "Funktionsweise und Beispiel"

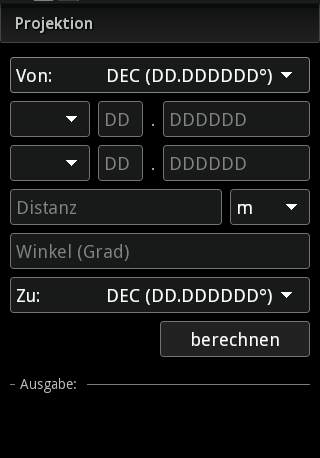
Eingabe
  1. Eingabe Informationen zur Koordinate
  2. Angabe des Entfernung sowie der Einheit der Entfernung [m, km, nm, ft]
  3. Angabe des Winkels (in Grad)
  4. Auswahl des Formates der ermittelten Koordinate
  5. Berechnung starten
Ausgabe
Koordinate des projizierten Punktes

Schnittpunkt zweier Linien aus vier Punkten



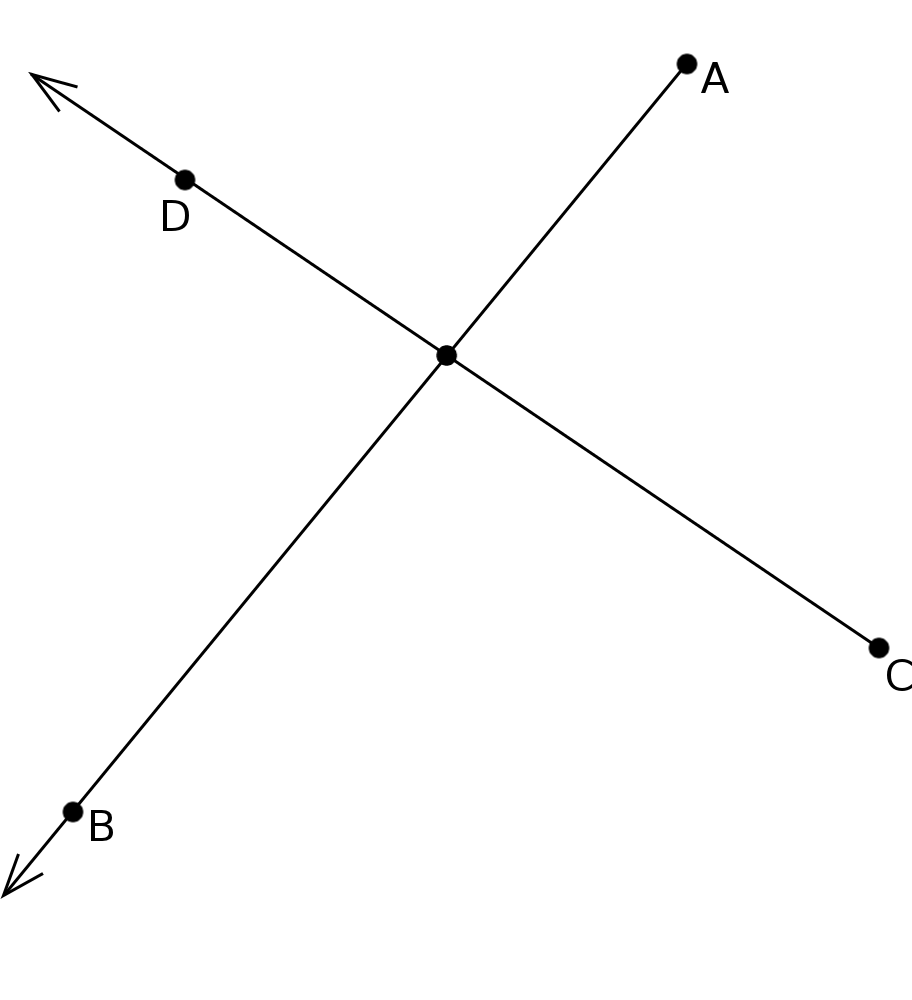
Für diese Funktion werden vier Punkte A, B, C, D benötigt. Je zwei werden zu Paaren zusammen gefasst (beispielsweise A und B, sowie C und D). Nun wird von A ein Strahl durch B geschickt und von C durch D. Die Funktion berechnet den Schnittpunkt dieser beiden Strahlen. Dieser muss nicht unbedingt innerhalb des Vierecks ABCD liegen, sondern kann bei geeigneter Wahl der Punktpaare auch außerhalb liegen (wenn die Linien nicht die Diagonalen sind).

Eingabe
  1. Eingabe Informationen zur Koordinate
  2. Angabe des Entfernung sowie der Einheit der Entfernung [m, km, nm, ft]
  3. Angabe des Winkels (in Grad)
  4. Auswahl des Formates der ermittelten Koordinate
  5. Berechnung starten
Ausgabe
Koordinate des ermittelten Schnittpunktes