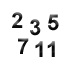vorherigerMenunächster

Primes

Functionality and example

A prime number is a natural number that is greater than one and can only be divided by itself and one. Therefor a prime number is a natural number with exactly two divisors. The smallest prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.

Prime factorization is finding which prime numbers multiply together to make the original number. For the number 45 the prime factorization would result in 3 * 3 * 5

Source: Wikipedia

Operation



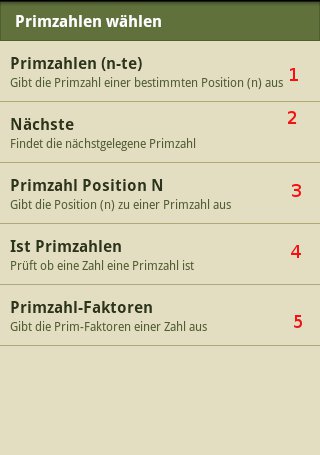
All following functions will branch out to an identical input system therefor there will be only a documention for one method. GCC operates with prime numbers that are smaller than 1000000.

Input
  1. Determination of the nth position of a prime number; Example: The 5th prime is 11
  2. Determination of the nearest prime number; Example: The nearest prime to 22 is 23. The nearest primes to 42 are 41 and 43.
  3. Determination of the position of a prime number; Example: The 5 is the 3rd prime.
  4. Check if a number is a prime number; Example: The 23 is a prime number, the 42 not.
  5. Prime factorization; Example: 42 = 2 * 3 * 7
Output

Determination of desired result



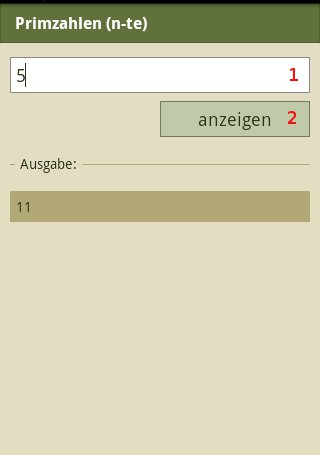
Input
  1. Entering of numerical value
  2. Running of calculation
Output
Display of the calculated numerical value or an error message if the entered value is not prime number