previous Menunext

Hash

Functionality and example

Hash functions will calculate hashs for strings (consisting of words or letters or numbers). Hashs look very much like arbitrary data strings. Hash functions will deliver data output of exactly the same length – no matter if only a letter, a word or a complete book are "hashed". A very important property of hashs is that they cannot be retraced.

Simplified speaking the reason is this: since all hashes have always the same length there can only be a limited number of them (For better understanding: There are also only a fixed number of 5digit numbers). Assuming a hash function returns hashs with the length of 2 digits, using only A and B, then there are only 2^2 = 4 different hashes: AA, AB, BA and BB. This function can get one of an infinite number of entries. And all of them are calculated into one of the four possible hash outputs. This is why it is impossible to retrace an entry value out of a hash value: There are infinite possibilies.

Hashes are often used in databases to store passwords for example. An access having person (like an attacker or simply the administrator) shouldn't read the passwords of the users. That's why only hashes of the passwords are stored. The person can't retrace the real password of the user out of the hash. Of course, in our example hash function it wouldn't be hard to find an entry that generates the same hash value as the user's password - nearly every forth possibilies does. But in reality hashes are much more complex. So the very important MD5 Hash has 128 bits, which means 2 signs and 128 digits. This results in 2^128 (ca. 3.4 * 10^38, a number with 38 digits) different hashes. To find one entry which generates the same one as the password's is too hard to calculate even for fast computers.

A second important property is the fact that hashes differ very from each other. So you can never say: "OK, this hash looks similar to that one. Than the entry of the first would be nearly the same then the one of the second hash." It's wrong, only one changed letter in the entry string can cause a complete different hash output.

Hash function become safer very continuously. That means, there are always new hash functions which generate more "random" output with longer hashes.

Beispiele:

MD5("Geocaching") = 6acb9296d8d3758f6817558a07b95d85

MD5("GeoCaching") = f67b62ba5809b02c4f242c4fe6ae6555

Operation

Here we offer 22 different hash functions. Their handling is completely identical.

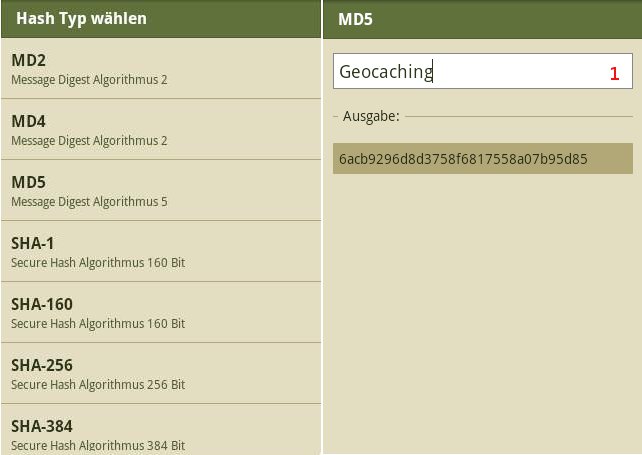
Input
  1. Input of the text to be encoded. The following hash functions can be chosen:
Output
Due to the chosen hash format calculated result.