vorherigerMenunächster

Coordinates

Functionality and Example

The definition of „coordinate“ is the description of a geological point in relation to a point of reference. A point on a ruler may have the coordinate "3 cm", which means that the point 3 cm is to be found 3 cm away from the start of the ruler at 0 cm, which would be the point of reference.

Assuming 2 dimensions such as a map, on also would need 2 specifications to be able to determine the point correctly: how far is the point to the left/right and up/down from the point of origin. This system can be expanded indefinitely, but in practise there are rarely more than a three-dimensional point of relevance (coordinates in space, with three entries).

Geographical coordinates are points in a geographic (earth-related) context. They describe points regarding to their position on earth. Since these are descriptions of places on the earth's surface, you need exactly two values??, therefor they are two-dimensional. One can visualize this fact can be on a (two-dimensional) map on which two values will be sufficient to find a city or something similar.

Geographical coordinates are not, however, measured in meters or other units of length, because the earth is not flat. One speaks of spherical bodies, for the first initial understanding of a ball. Therefore it is divided into a grid. The earth is split into 360 degrees of longitude and 180 degrees of latitude, that is, in mathematical angle. Longitudes run "vertically" through North and South Poles, latitude, "horizontally". The equator is the longest latitude, since this marks the thickest part of the earth. Therefore, the equator is the zeroth latitude. Starting here other latitudes to the North and the South are numbered. The poles, which are the northernmost or southernmost points of the earth lie at 90 ° north or south. The longitudes are counted from an arbitrary zero meridian to the east and west to 180 ° respectively. It was determined that the prime meridian runs through Greenwich / London, UK.

A place on Earth can therefor be determined by two numbers: how many degrees is it away from Greenwich to the east or west, and how many degrees north or south is it away from the equator.

Still one must keep in mind, that the earth is not a sphere, and therefore mathematical calculations on the surface (eg:. How long is the distance from point A to point B on the surface, also known simply as the distance between two locations) are not identical with the relatively simple spherical calculations. Rather, one uses another geometric object, called the ellipsoid. This is basically a flattened ball. Unfortunately, calculations for such an object the unreasonably complex. But on the assumption that the earth is identical to a ball, there could be errors up to 20km difference.

Still, an ellipsoid also is only an approximation, since the earth, caused by mountains and ocean depths, is not completely flat. Therefor this also causes computational discrepancies at some places. For this reason special ellipsoids which are locally adapted are used, for example the Bessel ellipsoid for Central Europe.

Today usually the ellipsoid WGS84 (World Geodetic System 1984) is used internationally, which represents the current best average approximation for the entire earth. This system also is standard with GPS (Global Positioning System) and Geocaching applications.

The GPS coordinates of a point are given in degrees (°), minutes (') and seconds (") As with time: = 1 ° 60' and 1 '= 60". Possible representations are:And here is a mnemonic: "N" (or "S") is the latitude, "O" (or "W) is the longitude.

Source: Wikipedia

Geocaching and Coordinate Projection

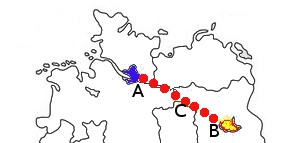
For many mysteries it is necessary to perform a projection. In order to understand the basic procedure there will be an example. The projection is made up information of an angle and a distance. To understand the angular data, one can imagine a compass with the following angles:Assuming you are in Hamburg (blue mark) and you want to make a projection (red line) to Berlin (yellow mark), the angle would be approx. 115° and a distance of 256 km. Starting in Berlin the location of Hamburg can be found by using an angle of approx. 298° and – surprise!! – also 256 km.

Bedienung

Anmerkung zur Bedienung

In the following descriptions for each coordinate first the format of the coordinates should be chosen: This is followed by entering latitude and longitude for each coordinate. For DEC only one algebraic sign instead of N / S or E / W is required. The following applies: South and West are negative, North and East positive.

Input
  1. Calculate the angle between two coordinates
  2. Convert different coordinate formats
  3. Calculate distance between two coordinates
  4. Geohash (latitude/longitude geocode)
  5. Calculate the intersection point using angles
  6. Calculate the intersection point based on distances (two)
  7. Calculate the intersection point based on distances (three)
  8. Calculate the intersection point using angle and distance
  9. Calculate the intersection of two lines of four basis points
  10. Determine the center of two coordinates
  11. Projection of a coordinate on a specified distance

Calculation of two coordinates in relation to each other

After determining the longitude and latitude of two points A and B, it can be calculated in which direction B lies in relation to A and vice versa (for example, if you want to know the direction you could find Hamburg whilst being in Berlin). The compass will be used as reference. 0 ° would mean that Hamburg would be located directly in the north – which it obviously does not :-)

On a simple level, the forward and reverse direction would differ by 180 ° (half turn). This result is not possible in spherical calculations. There will be deviations due to the curvature.


Input
  1. Information to the first coordinate
  2. Information to the second coordinate
  3. Start calculation
Output
The calculated angle of the forward and reverse direction relative to North = 0 °.

Convertion between different coordinate formats

Conversion from DEC in DEG or conversion of other formats. DEC, DEG and DMS are strongly related to each other. Examples: The reverse direction is similar: The conversion to UTM and MGRS are much more complex and can be found in appropriate literature.

Input
  1. Input information for the first coordinate
  2. Selection of the desired coordinate format
  3. Start calculation
Output
Convertion of the desired format coordinate

Calculation of distance between two coordinates

This function gives the shortest distance between two points. It does not matter which is the point of origin and which the target point.

input
  1. Input information for the first coordinate
  2. Selection of the desired coordinate format
  3. Start calculation
Output
Distance between the coordinates

Geohash (latitude/longitude geocode)

Geohash is used to specify the coordinates of a point with a short and unique identifier, so that the coordinate information in emails, forums, etc. becomes easier. It was developed by Gustavo Niemeyer, it was published on geohash.org. The calculation is based on a transformation of coordinates in Base32 and a further transformation of the binary values.

Input
  1. Selection of the mode (encode, decode)
  2. Entering of the coordinate (with format selection) or the Geohash
  3. Selection of the coordinate format (for decode)
  4. Start calculation
Output
Geohash or coordinate in the desired format

Calculation of an intersection point using angles



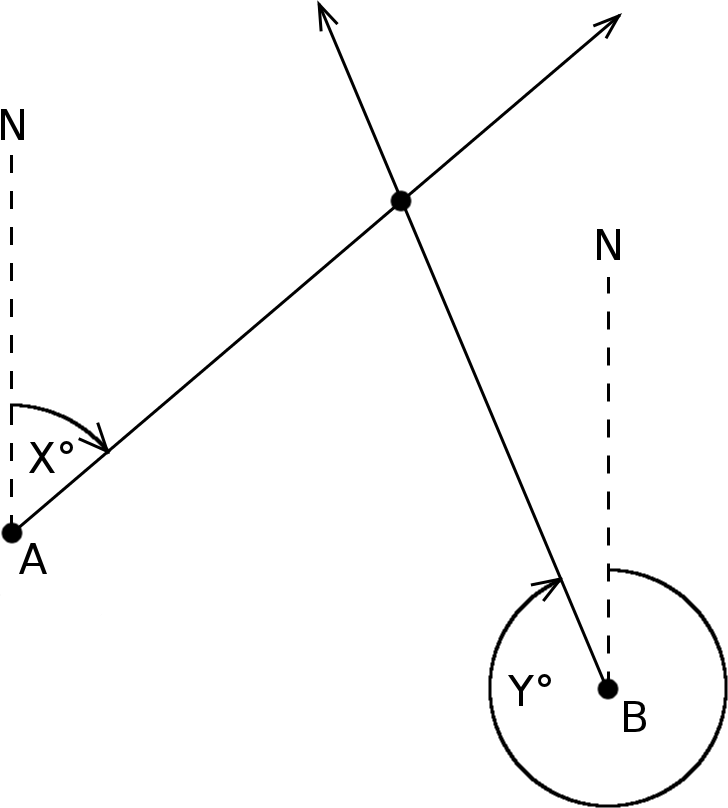
This calculation is based on the classic "cross bearing" based as it is mainly used in shipping. A ship can determine its position by homing in on two fixed points – thereby using the compass to assesss in direction they lie. Thus, the lighthouse may be at 270 ° lie and the buoy at 15 °. This gives us a distinct point. Would the ship move on the direction of the tower and the buoy would also change. This feature does the opposite: it looks for the ship. I you know, the ship is so many degrees from the lighthouse and so many degrees away from the buoy.One could think a (sufficiently long) line from lighthouse and buoy in the appropriate direction. Where the two lines meet, the ship is located - or, of course, much better: the cache! :)


Input
  1. Input information for the first coordinate)
  2. Indication of the angle (in degrees)
  3. Input information for the second coordinate
  4. Indication of the angle (in degrees)
  5. Select the format of the determined coordinate
  6. Start calculation
Output
Coordinate of the calculated intersection

Calculation of the intersection point on the basis of distances



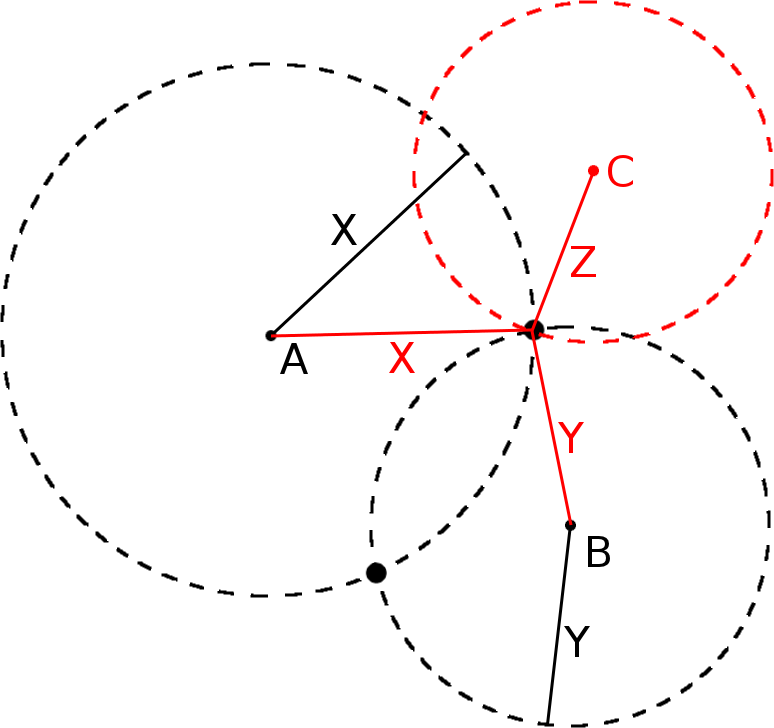
2 Points

To understand this function, we pretend to move on level land like on a map. We know that the cache is somewhere. We have only two pieces of information: it is X meters away from the birch and Y meters from the oak. But there is one problem: Suppose we are at the birch. We would know that we have to go X meters, but in which direction? It’s the same with the oak. We are looking for the point which meets both conditions. How to do this? Well, simply put, we can look for the birch on our map and draw a circle of radius X around it. All points of the circle are the possible intersection points, which are precisely X meters away from the birch. The same should be done with the oak. And now if we are lucky, the two circles touch at one point. This point is also part of the birch and the oak circle, so it is X meters from the birch, and Y meters away from the oak.

Das gleiche erhält man, wenn man das gleiche mit der Eiche macht. Und wenn wir nun Glück haben, berühren sich die beiden Kreise in einem Punkt. Dieser Punkt ist also Teil des Birken- als auch des Eichenkreises, ist also X Meter von der Birke, als auch Y Meter von der Eiche weg.

However, it is more likely that the two circles intersect either not at all (that would be bad, right? Then you should have another look at the task * gg *) or in two points. Which point is it now? It is impossible to tell. The only solution now: trial and error! Unless ...

3 Points

you still have another specification, a third point. Maybe the cache also to be Z meters away from the pine tree? draw a third circle around the pine tree. If you are lucky, this one runs through the first two intersections.

Notes:
  1. Due to measurement and computing inaccuracies, the calculation of the third circle will only be an approximation: Inaccurate coordinate data may result in a deviation of the circle of one meter or so. Here is room for tolerances which acceptability has to be assessed by the user.
  2. Also, the three-point method may in rare case result also in two intersections, namely if the third point lies exactly on the imaginary line connecting the first two points. Then there is either no or two points of intersection of the three circles.


Input
  1. Input the first coordinate
  2. Indication of the distance and unit distance [m, km, nm ft]
  3. Input information of the second coordinate
  4. Indication of the distance and unit distance [m, km, nm ft]
  5. Select the format of the determined coordinate
  6. Start calculation
Output
2 Points
The calculated coordinates and the coordinates of the intersection of two intersections.
3 Points
Regular output: When an intersection point / multiple intersection points within the specified tolerance are found, their coordinates are displayed.
Extended Output: In the calculation two sets overlap each other. At the most this could result in six intersections. For all intersections the distance to third coordinate will be determined. The extended output will give all intersection coordinates including their distance to the third coordinate, as "tolerance". If this distance is within the specified tolerance it is considered a "hit". The intersection points are sorted in ascending order according to their tolerance.

Calculation of the intersection point using angle and distance



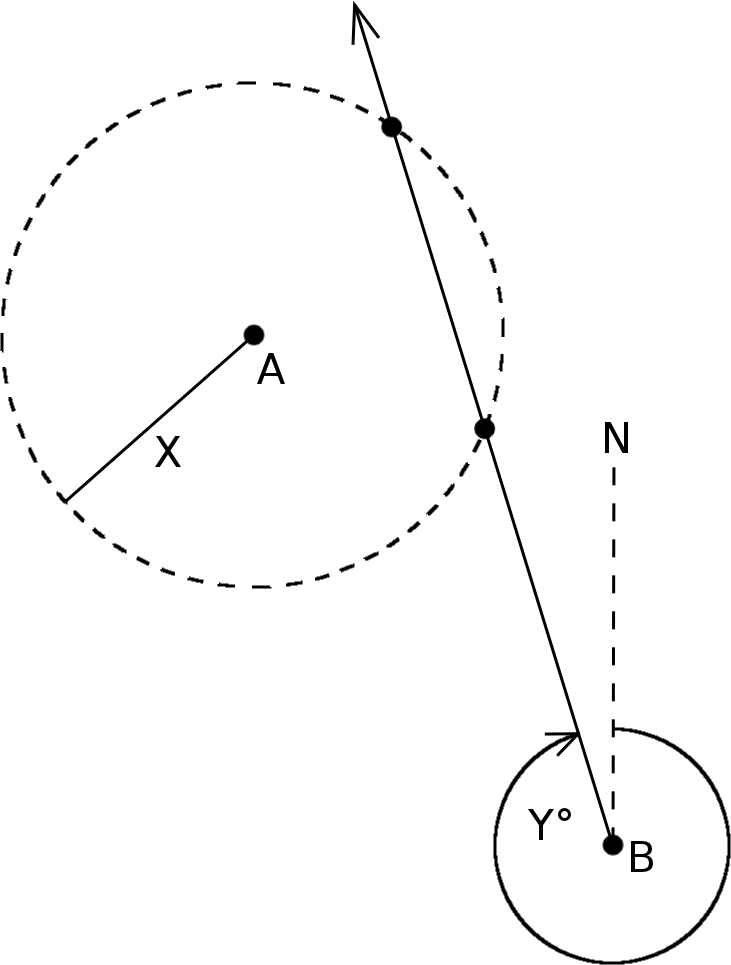
This is the scenario: We know that the cache is located X feet away from a certain point A, for example a building. However, we do not know in which direction. One could draw a circle around the house, with the radius of X. Somewhere on the circle must now be the cache. But now you have a second information: Starting at the chimney (or any other point B) you have to walk in Y degrees. However you don't know how far. So now you walk in the direction Y. If you are lucky, you will cross the previously drawn circle. That is the point where the cache is: Exactly X meters from the house and Y degrees from the chimney.

In most cases two intersections are calculated since the line runs usually through the range circle (this is called a secant). In rare cases, it actually touches only one point, then it is a tangent. In case of incorrect assignment (wrong reading is not even in question!) there will be no intersection. Then the line is called a passant.

Input
  1. Input information for the first coordinate
  2. Indication of the angle (in degrees)
  3. Input information for the second coordinate
  4. Indication of the distance and unit distance [m, km, nm ft]
  5. Select the format for the determined coordinate
  6. Start calculation
Output
Coordinate(s) of the calculated intersection point(s)

Determination of the midpoint of two coordinates

The following picture determines the coordinates of point C, which lies midway between the points A and B.



Eingabe
  1. Input information for the first coordinate
  2. Input information for the second coordinate
  3. Select the format of the determined coordinate
  4. Start calculation
Output
Coordinate of the calculated midpoint

Projection of a coordinate on a specified distance

See Example in chapter: “Functionality and Example”

Input
  1. Input information for coordinate
  2. Indication of the distance and unit distance [m, km, nm ft]
  3. Indication of the angle (in degrees)
  4. Select the format of the determined coordinate
  5. Start calculation
Output
Coordinate of the projected point

Intersection of two lines of four points



For this function four points A, B, C, D are needed. Two each are taken together to form pairs (eg A and B, and C and D). Now a line from A to B, and another line from C to D is drawn. The function calculates the intersection of these two lines. This does not necessarily lie within the square made by ABCD, but can be outside when choosing approbiate points (if the lines are not the diagonals).

Input
  1. Input information for coordinate
  2. Indication of the distance and unit distance [m, km, nm ft]
  3. Indication of the angle (in degrees)
  4. Select the format of the determined coordinate
  5. Start calculation
Output
Coordinate of the calculated intersection