vorherigerMenunächster

Zahlensystem

Funktionsweise und Beispiel

Zahlensysteme werden zur Darstellung von Zahlen verwendet. Eine Zahl wird entsprechend der Regeln des jeweiligen Zahlensystems als Folge von Ziffern bzw. Zahlzeichen dargestellt. Unser Zahlensystem (Dezimalsystem) ist ein Stellenwertsystemen (Im Gegensatz zu den Additionsystemen, bei denen einfach alle Ziffern, unabhängig ihrer Position aufsummiert werden; Bsp: Strichliste auf Bierdeckeln). Stellenwertsystem heißt, dass Ziffern an unterschiedlichen Stellen, unterschiedliche Wertigkeiten haben: Bei den Ziffern 1 und 9 ist es von Bedeutung, wo welche steht, das hat Einfluss auf deren Wertigkeiten: 19 oder 91.

Doch es gibt noch mehr Stellenwertsysteme, als die auf die Zehn aufgebaute Variante (man sagt: "Zur Basis 10"). Bekannt ist das System zur Basis 60 (Sexagesimalsystem) von der Uhrzeit. Während im Zehnersystem bis 9 gezählt wird, bevor die nächste Stelle "umgeschaltet" wird, wird bei der Uhr bis 60 gezählt, bevor die nächste Stelle weiterrückt: 60 Sekunden machen eine Minute und 60 Minuten machen eine Stunde.
Dass sich bei uns das Zehnersystem eingebürgert hat, wird allgemein auf die zehn Finger zurück geführt, die man zum Rechnen verwenden kann. Doch finden sich in Mittelamerika Hinweise auf die Nutzung des Zwanzigersystems (zusätzliche Nutzung der Zehen). Auch in Frankreich finden sich Hinweise auf dieses so genannte Vigesimalsystem: Die französischen Zahlworte basieren auf dem Zwanzigersystem.
Das heute bedeutendste System ist das Binärsystem (von "bi" wie 2). Computer rechnen intern nur mit zwei Zeichen, der 0 und der 1. Und so müssen alle Daten erst in das Binärsystem umgerechnet werden, bevor sie verarbeitet oder gespeichert werden können. Damit dürfte die Umrechnung von Dezimal in Binär die häufigste heute getätige Umwandlung von Stellenwertsystemen sein.

Um die Umrechnungen zu verstehen, muss man sich noch einmal (auch wenn es banal aussieht) verdeutlichen, wie unser Zahlensystem im Grunde funktioniert: Im Dezimalsystem hat man zehn Ziffern zur Verfügung. Diese stehen an bestimmen Stellen, wie der Einerstelle (die nullte Stelle: 10^0 = 1) oder der Hunderterstelle (die zweite Stelle: 10^2 = 100). Ist man beim Zählen an einer Stelle von 0 bei 9 angekommen, wird die nächste Stelle um eins hochgezählt und die aktuelle Stelle fängt wieder bei Null an: Bei System mit nur zwei Zeichen (zum Beispiel 0 und 1) geht das genauso, nur eben mit einer geringeren Anzahl von verwendeten Zeichen: Doch wie kann man sich höhere Zahlensysteme vorstellen? Es gibt doch nur 10 Ziffern. Ja, richtig, aber nur, weil wir gewohnt sind, nur diesen Zeichen einen mathematischen Wert anzuerkennen. Man kann auch ganz einfach neue Zeichen einführen. Im in der Informatik häufig verwendeten Sechzehnersystem (Hexadezimalsystem) gibt es in der Tat 16 Ziffern: Nach der 9 folgen A, B, C, D, E und F (gleich 10 bis 15, insgesamt also 0-9A-F = 16 Zeichen). Es wird also gezählt: 98, 99, (nicht 100, denn auf 9 folgt A) 9A, 9B, 9C, 9D, 9E, 9F, (immernoch nicht 100, denn auch bei höheren Stellen folgt auf die 9 das A) A0, A1, A2, ..., A9, AA, ..., AF, B0, ..., FE, FF, (jetzt sind die Zeichen verbraucht, also) 100.

Die Darstellung von Zahlen in Zahlensystem erfolgt mittels Exponentendarstellung: A * B^C. A ist der Wert der Stelle, B das Basissystem und C die Stelle. Die 123 lässt sich wie folgt darstellen:
123 = 1 * 10^2 + 2 * 10^1 + 3 * 10^0 = 1 * 100 + 2 * 10 * 3 * 1
Dies ist in anderen Zahlensystemen identisch. Eine Binärzahl wird genauso gewertet, nur mit der 2 in der Basis anstelle der 10: 1111011 = (1 * 2^6 + 1 * 2^5 + 1 * 2^4 * 1 * 2^3 + 0 * 2^2 + 1 * 2^1 + 1 * 2^0) = (1 * 64 + 1 * 32 + 1 * 16 + 1 * 8 + 0 * 4 + 1 * 2 + 1 * 1). Und das zusammengerechnet ergibt unser Beispiel von oben: 123. So sieht die Umwandlung von Binär zu Dezimal aus.


Man kann natürlich auch Kommazahlen im Stellenwertsystem darstellen. Wie man vermuten kann, wenn man sich die Summanden anschaut, haben die Nachkommastellen negative Exponenten. So ist 23,42 im Zehnersystem:
2 * 10^1 + 3 * 10^0 + 4 * 10^(-1) + 2 * 10^(-2)
Natürlich lassen sich auch Kommazahlen in andere Zahlensysteme umrechnen. Doch die Mathematik dahinter sprengt diesen Rahmen.
Um das Ganze noch zu toppen, gibt auch negative Zahlensysteme. Man nennt diese Basen dann Negabasen. Aber auch das nur als Anmerkung.

Beispiele

10111,001 (binär) = 1 * 2^4 + 0 * 2^3 + 1 * 2^2 + 1 * 2^1 + 1 * 2^0 + 0 * 2^(-1) + 0 * 2^(-2) + 1 * 2^(-3) = 1 * 16 + 0 * 8 + 1 * 4 + 1 * 2 + 1 * 1 + 0 * (1/2) + 0 * (1/4) + 1 * (1/8) = 16 + 4 + 2 + 1 + (1/8) = 23,125 (dezimal)
19 (Basis 23) = 1 * 23^1 + 9 * 23^0 = 32 (dezimal) = W (Basis 42); heißt W ist das 32. Zeichen: 0123456789ABCDEFGHIJKLMNOPQRSTUVW --> stimmt ;)
38 (dezimal) = c (Basis 42); heißt a ist 36. Zeichen: 0123456789ABCDEFGHIJKLMNOPQRSTUVabc
85 (dezimal) = 21 (Basis 42); heißt 2mal 42 Zeichen durchgezählt (= 84) und auf die nächste Stelle übertragen und dann von vorn angefangen, fehlte ja noch ein Wert bis 85
174 (Basis -10) = 1 * (-10)^2 + 7 * (-10)^1 + 4 * (-10)^0 = 1 * 100 + 7 * -10 + 4 * 1 = 100 - 70 + 4 = 34 (dezimal)

Bedienung

GCC bietet folgende Umrechnungen:

Eingabe
  1. Umwandeln von Zahlen in mehrere Zahlensysteme gleichzeitig
  2. Umwandeln von Zahlen von einem Zahlensystem in ein anderes
  3. Anzeigen der Tabelle mit Namen verschiedener Zahlensysteme

Umwandeln von Zahlen in mehrere Zahlensysteme gleichzeitig



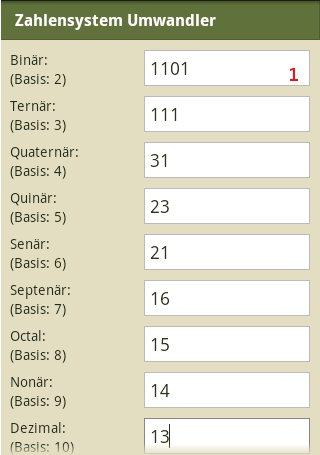
Eingabe
  1. Eingabe einer Zahl in ein beliebiges Eingabefeld (Achtung; Jede Ziffer muss kleiner sein als die zugehörige Basiszahl [bei Basis 5 ist die größte verwendbare Zahl 4])
Ausgabe
Darstellung der Zahl in allen anderen Zahlensystemen

Umwandeln von Zahlen von einem Zahlensystem in ein anderes



Eingabe
  1. Eingabe einer Zahl, die umgewandelt werden soll
  2. Auswahl des Zahlensystems der eingegebenen Zahl
  3. Auswahl des Zahlensystem, in das umgewandelt werden soll
Ausgabe
Die umgewandelte Zahl

Anzeigen der Tabelle mit Namen verschiedener Zahlensysteme



Eingabe
-
Ausgabe
Anzeige der Tabelle mit den Namen verschiedener Zahlensysteme