Alphanumerisch

Funktionsweise und Beispiel

Jeder Buchstabe hat eine bestimmte Stelle im Alphabet. A ist der 1. Buchstabe, B der 2. und Z der 26. Also bekommt A den Wert 1 und Z den Wert 26. Möglich sind auch andere Zählweisen. So kann man die Werte einfach verschieben. Mit einem Versatz von 2 hat A den Wert (Normalwert 1 + Versatz 2) = 3 und Z = 26 + 2 = 28. Auch ist es möglich, die Wertigkeiten umzudrehen, also A = 26 und Z = 1.
Die häufigste und einfachste Variante (A=1, Z=26) findet sich sehr häufig in Multis und Mysteries als einfache Zahlenverschlüsselung.

Mit diesen Zahlen können eine Menge Berechnungen angestellt werden, wie die Addition der Buchstabenwerte. Deshalb werden einfache in dieser Funktion mit ausgegeben, wie die Quersumme. Als Quersumme (oder Ziffernsumme) bezeichnet man die Summe der Ziffernwerte einer Zahl. So ist für eine Zahl n = 36036 die dezimale Quersumme q(n) = 3 + 6 + 0 + 3 + 6 = 18.

Die Quersummenbildung wird im Geocaching häufig genutzt, um z.B. bei Multis aus einer Zeichenfolge Zahlenwerte zu ermitteln. Für jeden Buchstaben wird dann der zugehörige Zahlenwert zur Quersumme addiert.

Analog dazu werden beim Querprodukt die Ziffern multipliziert.

Achtung: Da es verschiedene Arten der Quersummenberechnung gibt, muss man genau lesen, was z.B. in der Cachebeschreibung gemeint ist!

Beispiele:

Beispiele für Buchstabenwerte:

Modus Text zu Zahlen, Vorwärts, Versatz 0: ABC = 1 2 3
Modus Text zu Zahlen, Vorwärts, Versatz -10: ABC = (1 - 10) (2 - 10) (3 - 10) = -9 -8 -7
Modus Text zu Zahlen, Rückwärts, Versatz 10: ABC = (26 + 10) (25 + 10) (24 + 10) = 36 35 34
Modus Text zu Zahlen, Rückwärts, Versatz -100: ABC = (26 - 100) (25 - 100) (24 - 100) = -74 -75 -76
Modus Zahlen zu Text, Vorwärts, Versatz 0: 1 2 3 = ABC
Modus Zahlen zu Text, Rückwärts, Versatz -100: -74 -75 -75 = (-74 + 100) (-75 + 100) (-75 + 100) = 26 25 24 = ABC

Beispiel für Quersummen (für den einfachen Modus A=1, Z=26):
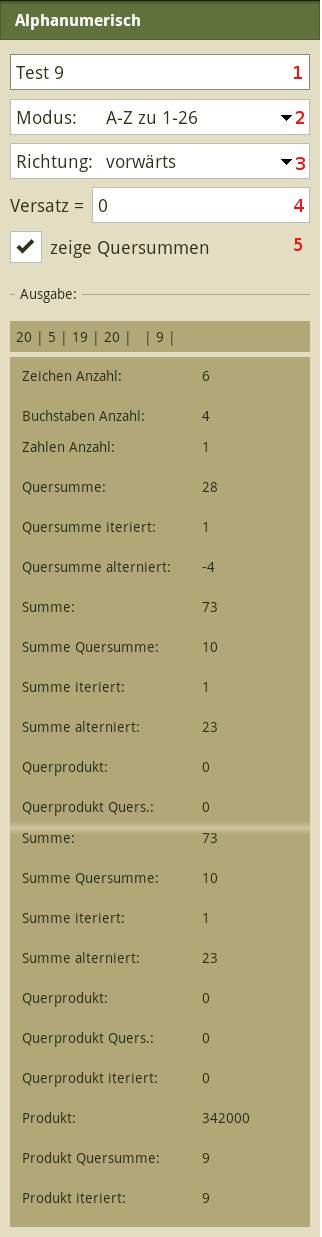
Für den Text "TEST 9" werden, wenn A=1... Z=26 ist, die Zahlen 20, 5, 19, 20, [LEERZEICHEN], 9 ermittelt. Damit ergeben sich:

die Zeichen Anzahl: 6
die Buchstaben Anzahl: 4
die Zahlen Anzahl: 1
die Quersumme der Ziffern: 2 + 0 + 5 + 1 + 9 + 2 + 0 + 9 = 28
die iterierte Quersumme, d.h.die Bildung der Quersumme auf der ermittelten Zahl solange, bis sie einstellig ist: 28 -> 2 + 8 = 10 -> 1 + 0 = 1 (auch "einstellige Quersumme" genannt)
die alternierende Quersumme, d.h. es wird abwechselnd vom letzten Zeichen beginnend subtrahiert und addiert: 9 - 0 + 2 - 9 + 1 - 5 + 0 - 2 = -4
die Summe der Zahlen: 20 + 5 + 19 + 20 + 9 = 73
die Quersumme der Summe: 73 -> 7 + 3 = 10
die ueber die Summe iterierte Quersumme: 73 -> 7 + 3 = 10 -> 1 + 0 = 1
die ueber die Zahlen alternierende Quersumme: 9 - 20 + 19 - 5 + 20 = 23
das Querprodukt: 2 * 0 * 6 * 1 * 9 * 2 * 0 * 9 = 0
die Quersumme des Querproduktes: 0 (angenommen Querprodukt war 83, dann ergäbe es hier: 8 + 3 = 11)
die iterierte Quersumme des Querproduktes: 0 (angenommen Querprodukt war 83, dann ergäbe es hier: 8 + 3 = 11 -> 1 + 1 = 2)
das Produkt der Zahlen: 20 * 5 * 19 * 20 * 9 = 342000
die Quersumme über das Produkt: 3 + 4 + 2 + 0 + 0 + 0 = 9
die iterierte Quersumme über das Produkt: 9 (angenommen Quersumme des Produktes war 10, dann ergäbe es hier: 10 = 1 + 0 = 1)

Quelle: Wikipedia

Bedienung

Es ist möglich, Text in Zahlen (Buchstaben werden zu deren Stellenwerten, Ziffern bleiben Ziffern, Sonderzeichen werden bis auf "Anzahl Zeichen" ignoriert) umzuwandeln. Ebenso funktioniert die Rückrichtung Zahlen in Text. Dort bekommt jede Zahl seinen Buchstaben zugewiesen. Auch da funktioniert die Quersummen-Erweiterung - es werden die Eingaben berechnet.

Eingabe

Umzusetzende Buchstaben- oder Zahlenfolge. Beim Modus (1-26 zu A-Z) müssen zwischen den Buchstabenwerten Leerzeichen gemacht werden, da bei 123 nicht unterschieden werden kann, ob es ABC oder (12 = L)C oder A(23 = W) ist.
Modus (A-Z zu 1-26, also Text zu Zahlen, oder 1-26 zu A-Z, also Zahlen zu Text). Achtung: Die Auswahl des Modus sollte zuerst erfolgen, da sie das Eingabefeld der Ziffernfolge löscht!
Richtung der Umsetzung (vorwärts: A=1 und Z=26, rückwärts: A=26 und Z=1)
Eingabe eines Versatzes, der zusätzlich auf die ermittelte Zahlenfolge addiert wird
Checkbox, ob Quersummen angezeigt werden soll.

Ausgabe
Ermittelte Zahlen - oder Buchstabenfolge und ggf. Quersummen der ermittelten Zahlenfolge (zur Erläuterung siehe Funktionsbeschreibung "Quersumme")